定理内容
歐拉函數的展開式如下:
即
歐拉函數展開後,有些次方項被消去,隻留下次方項為1, 2, 5, 7, 12, ...的項次,留下來的次方恰為廣義五邊形數。若将上式視為幂級數,其收斂半徑為1,不過若隻是當作形式幂級數來考慮,就不會考慮其收斂半徑。
和分割函數的關系
歐拉函數的倒數是分割函數的母函數,亦即:
其中 為k的分割函數。上式配合 五邊形數定理,可以得到:
考慮 項的系數,在
時,等式右側的系數均為0,比較等式二側的系數,可得:因此可得到分割函數
的遞歸式以
為例
歐拉函數的展開式如下:
即
歐拉函數展開後,有些次方項被消去,隻留下次方項為1, 2, 5, 7, 12, ...的項次,留下來的次方恰為廣義五邊形數。若将上式視為幂級數,其收斂半徑為1,不過若隻是當作形式幂級數來考慮,就不會考慮其收斂半徑。
歐拉函數的倒數是分割函數的母函數,亦即:
其中 為k的分割函數。上式配合 五邊形數定理,可以得到:
考慮 項的系數,在
時,等式右側的系數均為0,比較等式二側的系數,可得:因此可得到分割函數
的遞歸式以
為例上一篇:歐拉積分
下一篇:高歐拉商數
 電位滴定儀
電位滴定儀
 色度儀
色度儀
 透光石
透光石
 歐拉積分
歐拉積分
 59
59
 2010
2010
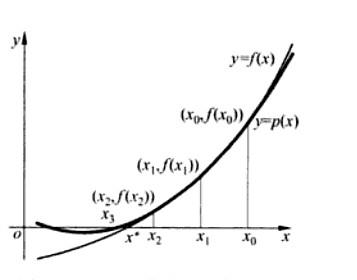 馬勒法
馬勒法
 黑洞數
黑洞數
 211
211
 71
71
 308
308
 丘成桐猜想
丘成桐猜想
 畢達哥拉斯三元數組
畢達哥拉斯三元數組
 127
127
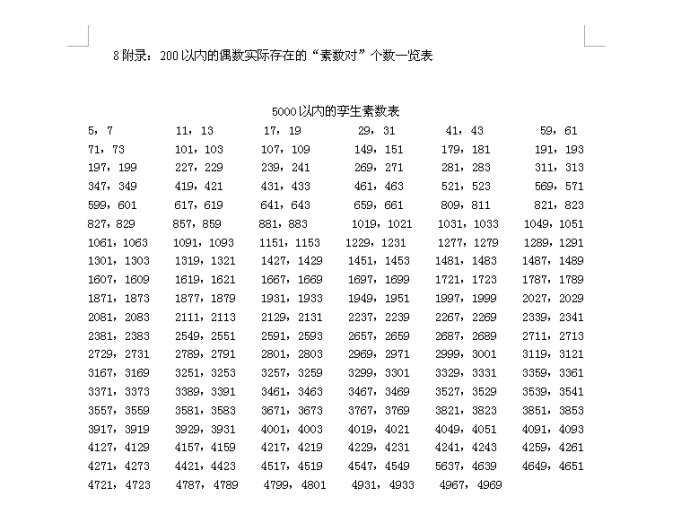 孿生素數表
孿生素數表
 n維歐幾裡得空間
n維歐幾裡得空間
 歐幾裡得度量
歐幾裡得度量
 表兄弟素數
表兄弟素數
 苗寶數
苗寶數
 帕斯卡法則
帕斯卡法則