基本介绍
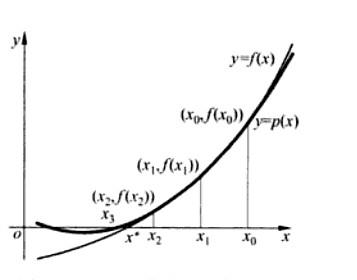
Muller方法的算法原理如图所示,对于求
的零点x'来说,假设已经得到互异的三个点处的函数值,那么可以 经过平面上的三个点以及作为抛物线,记为(图中较粗的那条曲线),并把抛物线与x轴的交点作为的近似解。接下来再经过,以及作为抛物线……从而形成一个算法,算法的关键是求抛物线与x轴的交点。假设过
以及这三个点的抛物线方程为 ************************************ (1)依次用
以及分别代入(1)式,得 ****************************(2) *************************** (3)*****************************(4)由(4)式可得
,分别代入到(2)(3)中,整理后得)********************** (5)********************** (6)为了把上面的方程组(5)(6)的解更有规律性,令
*************************************(7)把上面的定义的方程组分别代入(5)(6)中,整理后可得
***********************************************(8)再在(1)式中令
,利用求根公式解关于的方程可以得到************************* (9)************************ (10)由图可以看出,如果得到了插值抛物线的两个零点,应该取与
更靠近的哪一个最为问题的近似解。利用一元二次方程的求根的计算方法,可以得到 **************(11)上面的(11)式可以用来求下一个迭代点,其中a,b,c可以利用(7)式和(9)式得到,从而利用Muller方法求函数零点的关键问题得到解决。